Proiectarea și calculul autobasculantei cu vagon rotativ

Un dumper cu vagoane rotative poate fi mobil sau staționar.

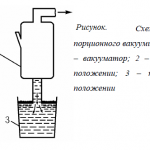
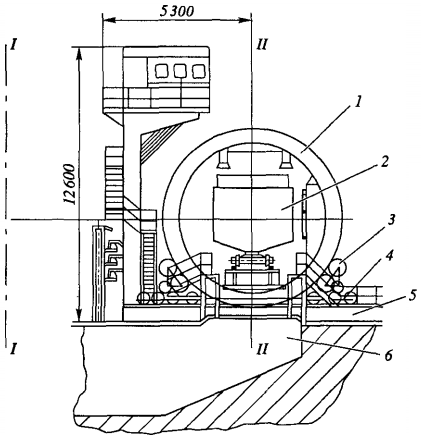
Dumperul de vagoane cu sens giratoriu mobil (figura 1) este realizat sub forma unei structuri metalice rotative circulare, ale cărei jante sunt montate pe cardanii 3, fixați pe podul 4. Podul este montat pe un număr de boghiuri care se deplasează pe șine 5. Într-o poziție (І-І), vagonul este împins în rotor de un împingător. În cealaltă ( ІІ-ІІІІ), rotorul 1 rotește vagonul, fixat în prealabil, cu 180° pentru a descărca încărcătura în șanțul sau buncărul 6. Spre deosebire de rotorul mobil, cel staționar are suporturile patinelor cu role fixate direct deasupra buncărurilor.

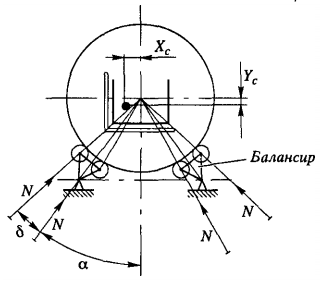
Schema de calcul a mecanismului de rulare este prezentată în figura 2.

Momentul total de rezistență la rulare al rotorului M = M₁ + М₂ . Momentul de rezistență M₁ din greutatea leagănului G_л și a vagoanelor G_в :

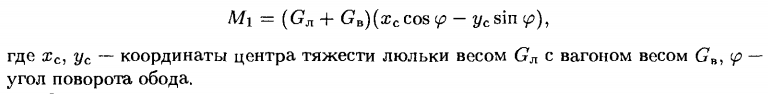
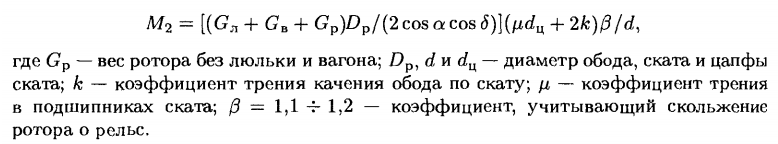
Cuplul static pe arborele motorului este determinat de raportul de transmisie i de la motor la angrenajul rotorului și este M _с = M/(iη) . Calculul suplimentar al mecanismului de rulare se efectuează în mod similar cu selectarea și testarea motoarelor pentru basculanta cu vagon turn.

Una dintre cele mai încărcate unități ale autobasculantei cu vagoane rotative este janta (sau bandajul) acesteia. Figura 3 prezintă schema de proiectare a rezistenței jantei.

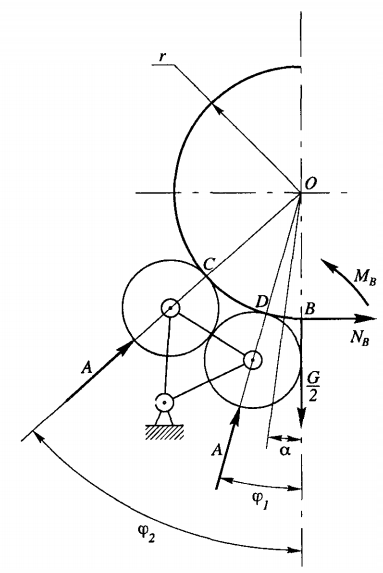
Condițional, vom considera sarcina G, provenind din greutatea rotorului, vagonului cu încărcătură, simetrică în jurul centrului O și aplicată pe jantă în punctul B . Forța orizontală N_в , forța tăietoare Q = G /2 și momentul M_в . Aici G este sarcina pe o jantă a basculantei. Pentru orice unghi de curent α ≤ φ₁ se stabilesc următoarele relații între parametri:

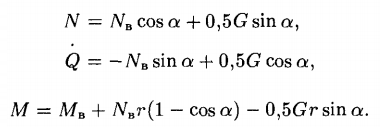
În intervalul de unghiuri φ₁ ≤ α ≤ φ₂ relațiile vor fi diferite:

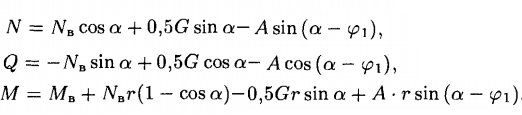
În cele din urmă, pentru intervalul φ₂ ≤ α ≤ π/2

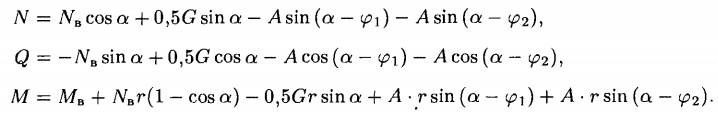
Pentru valorile standard φ₁ = 20° și φ₂ = 40° raportul 2A(cos40° + + cos20°)=G și răspunsul A = 0,293G .

Parametrii necunoscuți N_в și M_в ne permit să determinăm din condițiile ca în punctele C și D deformațiile y_в = y_D =0

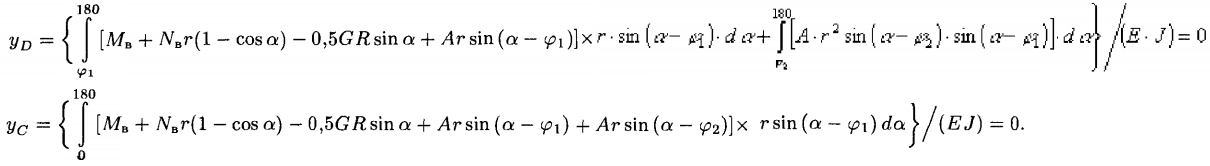
Soluția acestor ecuații este N _в = -0,151 G și Mv = 0,117 Gr . Din aceste date, se calculează încărcările relative de forfecare Q = Q/b, normală N = N/b și de moment M =M/(Gr) (tabelul 1).

Tensiuni maxime în orice secțiune a jantei

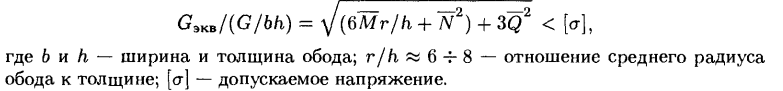
Tabelul 1 prezintă distribuția tensiunilor pe secțiunile transversale. Se poate observa din rezultate că cea mai mare tensiune va fi sub panta îndepărtată ( φ₂ = 40°):